Solutions

Blog

À propos

FAQ

Contact

Select Language

Connexion

Réserver une démo

8 déc. 2024

Optimisation des horaires de travail

Imaginez un entrepôt logistique qui fonctionne 24 heures par jour. À chaque heure, le nombre de colis à traiter varie, rendant crucial d'avoir le bon nombre de travailleurs pour garantir que tout est terminé à temps. Embaucher plus de personnel que nécessaire augmente les coûts. D'un autre côté, avoir trop peu de travailleurs peut conduire à des retards et à l'insatisfaction des clients.

Travailleurs Permanents vs Temporaires

Les entreprises comptent sur deux types de travailleurs :

Travailleurs Permanents: Personnel à temps plein avec plus d'expérience et d'efficacité.
Travailleurs Temporaires: Embauchés selon les besoins, ils sont plus coûteux et moins efficaces mais offrent de la flexibilité.

Le principal défi est de trouver l'équilibre idéal entre ces deux groupes pour répondre à la demande sans gaspiller de ressources.

Résoudre le Casse-tête avec des Modèles Mathématiques

Les chercheurs ont développé des modèles mathématiques pour déterminer la meilleure façon de dimensionner le personnel. Ils utilisent une technique appelée programmation linéaire en nombres entiers 0-1, qui, en termes simples, est une manière de représenter les décisions (comme « assigner un travailleur ou non ») à l'aide d'équations mathématiques.

Objectifs du Modèle

Minimiser le nombre total de jours de travail pour réduire les coûts de main-d'œuvre.
Satisfaire la demande horaire, en s'assurant qu'il y ait suffisamment de travailleurs pour chaque quart.
Respecter les contraintes, telles que ne pas dépasser le nombre maximum de jours de travail consécutifs pour les employés permanents et éviter de programmer un travailleur pour plus d'un quart par jour.

Algorithmes Intelligents pour l'Optimisation

Résoudre ces modèles mathématiques dans la pratique peut être très complexe, surtout lorsqu'on traite avec des centaines ou des milliers de travailleurs et de quarts. C'est là que les algorithmes intelligents entrent en jeu :

Algorithme Génétique: Inspiré par l'évolution naturelle, il crée plusieurs « solutions candidates » et combine les meilleures parties de chacune pour trouver la solution optimale au fil du temps.
Recuit Simulé: Basé sur le processus de chauffage et de refroidissement des métaux, il explore différentes solutions en acceptant occasionnellement des moins optimales pour éviter de rester bloqué et finalement trouver la meilleure solution globale.

Systèmes de Fabrication Reconfigurables

L'optimisation des programmations est cruciale dans les usines modernes, en particulier celles utilisant des Systèmes de Fabrication Reconfigurables (RMS). Ces systèmes peuvent être rapidement ajustés pour produire différents produits ou gérer des variations de la demande.

Défis Supplémentaires

Risques au Travail: Assurer la sécurité des travailleurs en tenant compte des risques liés aux machines, ainsi que de l'expérience et de la formation des employés.
Préférences des Travailleurs: Offrir des horaires flexibles peut augmenter la satisfaction et la productivité des employés.

Modèle Multi-Objectifs

Pour relever ces défis, les chercheurs ont développé un modèle visant à :

Minimiser le Temps Total de Production (Makespan): Garantir que les produits sont fabriqués dans les plus brefs délais.
Minimiser le Coût Total de Production: Incluant les coûts opérationnels et de main-d'œuvre.
Maximiser la Durabilité Sociale: Améliorer la sécurité et la satisfaction des travailleurs.

Solutions Avancées avec les Algorithmes Évolutionnaires

Pour résoudre ce modèle complexe, des algorithmes évolutionnaires avancés sont employés :

NSGA-II: Un algorithme multi-objectifs qui trouve efficacement des solutions optimales en considérant plusieurs objectifs simultanément.
AMOSA: Un autre algorithme multi-objectifs conçu pour une optimisation efficace dans des conditions complexes.

Aperçu de NSGA-II

Les algorithmes génétiques (AG) figurent parmi les méthodes d'optimisation métaheuristiques les plus largement utilisées et ont été appliquées à de nombreux domaines. Ils appartiennent à un groupe de techniques d'intelligence computationnelle inspirées par les principes de l'évolution, encodant les solutions potentielles en structures de type chromosome. En utilisant plusieurs opérateurs reproductifs, tels que le croisement et la mutation, les AG préservent les informations clés dans chaque chromosome tout en générant de nouvelles solutions candidates.

Pour relever les défis de l'optimisation multi-objectifs, les AG nécessitent un système de classement vectoriel pour identifier des solutions efficaces. L'une des méthodes de classement vectoriel les plus importantes combinées avec les AG est le tri non dominé. Introduite par Srinivas et Deb, cette approche - appelée NSGA - applique un tri non dominé pour aborder les problèmes multi-objectifs.

Cependant, NSGA présente trois principaux inconvénients :

La procédure de tri non dominé est longue et coûteuse en calcul.
Déterminer les paramètres de partage appropriés est difficile.
L'absence d'élitisme peut entraîner la perte de solutions de haute qualité une fois trouvées.

Pour surmonter ces limitations, Deb a développé NSGA-II. Les étapes principales de NSGA-II sont décrites dans l'algorithme suivant.

Au cours de l'étape de croisement, les gènes des chromosomes parents sont sélectionnés pour créer de nouveaux descendants. L'approche la plus simple consiste à choisir un point de croisement au hasard. Sans aucune modification, les valeurs du chromosome avant et après ce point sont directement transmises aux descendants, tandis que les valeurs entre les points choisis sont échangées entre les parents correspondants pour produire les nouvelles solutions.

# Pseudocódigo para um algoritmo genético baseado em NSGA-II

# Parâmetros necessários:
# population_size, total_iterations, crossover_probability, 
# mutation_probability

# 1: Geração da solução inicial aleatória
population = generate_initial_population(population_size)

# 2: Avaliar valores objetivos
evaluate_population(population)

# 3: Atribuir rank baseado em Pareto
pareto_sort(population)

# 4: Gerar população de descendentes
offspring = generate_offspring(population, crossover_probability, 
                               mutation_probability)

# 5: Seleção por torneio binário
selected_parents = binary_tournament_selection(population)

# 6: Crossover e mutação
offspring = apply_crossover_and_mutation(selected_parents, 
                                         crossover_probability, 
                                         mutation_probability)

# 7: Início das iterações
for iteration in range(total_iterations):
    # 8: Para pais e filhos na população
    combined_population = population + offspring

    # 9: Regenerar nova população utilizando crossover e mutação
    offspring = apply_crossover_and_mutation(combined_population, 
                                             crossover_probability, 
                                             mutation_probability)

    # 10: Cálculo do valor de aptidão (fitness) de toda a população
    evaluate_population(combined_population)

    # 11: Ordenar soluções usando mecanismo de ordenação não-dominado
    pareto_fronts = non_dominated_sorting(combined_population)

    # 12: Adicionar soluções à próxima geração, partindo da primeira fronteira
    next_population = []
    for front in pareto_fronts:
        if len(next_population) + len(front) <= population_size:
            next_population.extend(front)
        else:
            next_population.extend(select_by_crowding_distance(front, 
                                                               population_size - 
                                                               len(next_population)))
            break

    # 14: Selecionar pontos da fronteira inferior com alta distância de aglomeração (já realizado acima)
    # 15: Criar próxima geração
    population = next_population

    # 16: Seleção por torneio binário
    selected_parents = binary_tournament_selection(population)

    # 17: Crossover e mutação
    offspring = apply_crossover_and_mutation(selected_parents, 
                                             crossover_probability, 
                                             mutation_probability)

# 18: Fim das iterações

Aperçu de AMOSA

Bandyopadhyay a introduit une technique d'optimisation multi-objectifs basée sur le recuit simulé, connue sous le nom de AMOSA. Cette méthode utilise une structure d'archive pour produire un ensemble de solutions de compromis. Les auteurs ont conçu une procédure novatrice qui prend en compte le statut de dominance pour déterminer la probabilité de conserver une nouvelle solution candidate générée. Le pseudocode pour l'AMOSA adapté est présenté dans l'Algorithme 2

# Pseudocódigo para um Algoritmo de Otimização Multiobjetivo Baseado em Arquivo

# Parâmetros necessários:
# Tmax, Tmin, iter, α (alpha), temp = Tmax
# É necessário também uma razão de perturbação (perturbation ratio)
# Archive: coleção de pontos (soluções) já conhecidos

Current_points = random_selection_from(Archive)
temp = Tmax

while temp > Tmin:
    for i in range(iter):
        New_points = perturb(Current_points)

        # Se Current_points domina New_points
        if dominates(Current_points, New_points):
            # New_points = Current_points com alguma probabilidade
            if should_replace():
                New_points = Current_points

        # Se Current_points e New_points não dominam um ao outro
        if non_dominating(Current_points, New_points):

            # Se New_points é dominado por k pontos no Archive
            if dominated_by_k_points_in_archive(New_points, Archive):
                # New_points = Current_points com alguma probabilidade
                if should_replace():
                    New_points = Current_points

            # Se nenhum ponto no Archive domina New_points
            if no_point_in_archive_dominates(New_points, Archive):
                New_points = Current_points
                add_to_archive(New_points, Archive)
                remove_dominated_by(New_points, Archive)

        # Se New_points domina Current_points
        if dominates(New_points, Current_points):
            New_points = Current_points
            add_to_archive(New_points, Archive)
            remove_dominated_by(New_points, Archive)

    temp = temp * α

return Archive

AUGMECON-R : Une méthode exacte conçue pour aider à identifier l'ensemble des solutions efficaces (frontière de Pareto) pour les problèmes multi-objectifs.

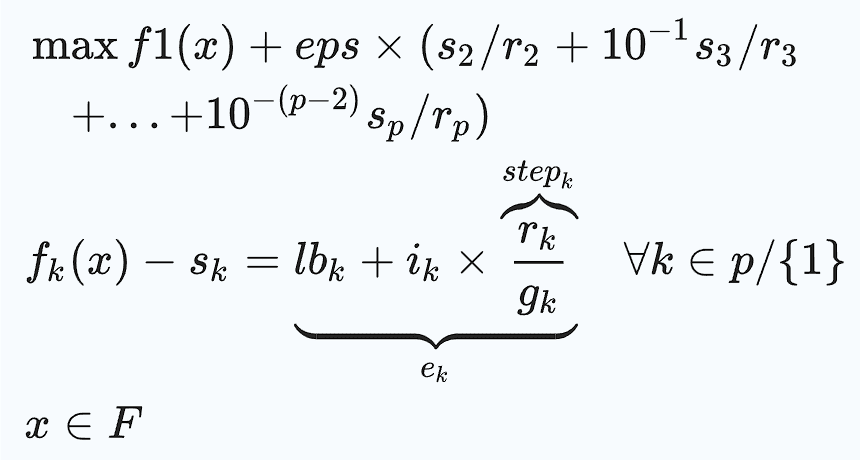
lbk désigne la borne inférieure du k-ème objectif, rk représente la plage du k-ème objectif, gk indique le nombre d'intervalles pour le k-ème objectif, et sk est la variable de relaxation associée au k-ème objectif. Le paramètre EPS est un très petit nombre, généralement choisi dans l'intervalle (10⁻⁶, 10⁻³), et F représente la région faisable. À chaque itération de l'algorithme, les coefficients de dérivation bi = int(si / stepi) sont calculés.

Si si ≥ stepi, alors l'itération suivante pour bi', où ei' = si - stepi, donnerait la même solution. Puisque si' = si - stepi, cette itération peut être considérée comme redondante. En d'autres termes, le coefficient de dérivation bi dicte combien d'itérations devraient être sautées.

Au cours de chaque itération de la boucle principale, l'algorithme maintient une matrice de drapeaux, flag[(g2 + 1) × (g3 + 1) × ... × (gp + 1)]. Initialement, cette matrice est réglée sur zéro. L'algorithme vérifie l'entrée de la matrice avant d'effectuer une optimisation : si l'entrée actuelle est nulle, elle procède à l'optimisation ; sinon, elle saute le nombre d'itérations spécifié par la valeur non nulle dans la matrice pour la boucle la plus interne.

Exemple Simple À l'Aide d'un Solveur Open Source

Description du Problème

Objectif : Minimiser le nombre total de jours de travail utilisés.

Travailleurs :

Travailleurs Permanents : Employés à temps plein avec des restrictions sur les jours de travail consécutifs.
Travailleurs Temporaires : Embauchés en fonction des besoins, sans restrictions sur les jours de travail consécutifs.

Demandes :

Variation quotidienne de la demande de travailleurs.
Besoin de répondre à la demande pour chaque journée de travail.

Contraintes :

Chaque travailleur peut faire un maximum d'un quart par jour.
Les travailleurs permanents ne peuvent pas travailler plus de 7 jours consécutifs.
Limites sur les heures travaillées par jour et par semaine.

Modélisation en Python

Ici, nous utilisons le modèle directement pour résoudre le problème, car nous traitons avec un petit nombre de travailleurs.

from pyomo.environ import *
from pyomo.opt import SolverFactory
import pandas as pd

# Dados do problema
dias = list(range(14))  # 14 dias
trabalhadores_permanentes = list(range(5))  # 5 trabalhadores permanentes
demanda = [8, 6, 7, 9, 10, 11, 9, 8, 6, 7, 9, 10, 6, 8]  # Demanda por dia
custo_permanente = 100  # Custo por dia de um trabalhador permanente
custo_temporario = 150  # Custo por dia de um trabalhador temporário

# Modelo
modelo = ConcreteModel()

# Variáveis
modelo.x = Var(dias, trabalhadores_permanentes, domain=Binary)  # Permanentes
modelo.y = Var(dias, domain=NonNegativeIntegers)  # Temporários

# Função objetivo: Minimizar custos
modelo.objetivo = Objective(
    expr=sum(custo_permanente * modelo.x[d, s] for d in dias 
             for s in trabalhadores_permanentes) +
         sum(custo_temporario * modelo.y[d] for d in dias),
    sense=minimize
)

# Restrições de demanda
modelo.restricao_demanda = ConstraintList()
for d in dias:
    modelo.restricao_demanda.add(
        sum(modelo.x[d, s] for s in trabalhadores_permanentes) + 
      modelo.y[d] >= demanda[d]
    )

# Restrição de no máximo 7 dias consecutivos para permanentes.
modelo.restricao_consecutivos = ConstraintList()
for s in trabalhadores_permanentes:
    for d in range(len(dias) - 7):
        modelo.restricao_consecutivos.add(
            sum(modelo.x[d + k, s] for k in range(8)) <= 7
        )

# Resolução
solver = SolverFactory('glpk')
resultado = solver.solve(modelo)

# Processamento dos resultados
custo_total = modelo.objetivo()

# Escalonamento de permanentes
escalonamento_permanentes = {
    f"Trabalhador {s + 1}": [int(modelo.x[d, s].value) for d in dias]
    for s in trabalhadores_permanentes
}

# Número de temporários por dia
temporarios = [int(modelo.y[d].value) for d in dias]

# Apresentar os resultados
print("Resultado da otimização:")
print(f"Custo total mínimo: R$ {custo_total:.2f}\n")

print("Escalonamento dos trabalhadores permanentes:")
for s in trabalhadores_permanentes:
    print(f"Trabalhador {s+1}: {escalonamento_permanentes[f'Trabalhador {s+1}']}")

print("\nNúmero de trabalhadores temporários por dia:")
for d in dias:
    print(f"Dia {d+1}: {temporarios[d]} temporários")

# DataFrame com o resultado final
resultado_df = pd.DataFrame(escalonamento_permanentes)
resultado_df["Temporários"] = temporarios
resultado_df["Demanda"] = demanda

print("\nTabela final:")
print(resultado_df)

Sortie :

Ces résultats montrent que le modèle a toujours utilisé les 5 travailleurs permanents pour le nombre maximum de jours consécutifs autorisés. Lorsqu'il était nécessaire de leur accorder collectivement un congé (pour éviter de dépasser la limite de travail consécutif de 7 jours), il s'est fortement appuyé sur les travailleurs temporaires pendant ce jour de repos. Cela a abouti à un schéma où de nombreux travailleurs temporaires étaient nécessaires certains jours (par exemple le jour 7) et peu ou pas d'autres, répondant à la demande mais de manière concentrée et moins réaliste d'un point de vue opérationnel.

Ceci est un exemple de code Python + Pyomo semblable au précédent, mais forçant une approche de planification plus réaliste. Pour y parvenir, nous avons ajouté des contraintes assignant des jours de repos spécifiques à chaque travailleur permanent (au lieu de permettre au solveur de décider librement, ce qui avait auparavant conduit tous les travailleurs à prendre le même jour de congé). Avec ces contraintes, chaque travailleur a un jour de repos décalé, empêchant tous les travailleurs permanents de devoir se reposer simultanément.

Le travailleur 1 se repose le Jour 4
Le travailleur 2 se repose le Jour 5
Le travailleur 3 se repose le Jour 6
Le travailleur 4 se repose le Jour 7
Le travailleur 5 se repose le Jour 8

from pyomo.environ import *
from pyomo.opt import SolverFactory
import pandas as pd

# Dados do problema
dias = list(range(14))  # 14 dias
trabalhadores_permanentes = list(range(5))  # 5 trabalhadores permanentes
demanda = [8, 6, 7, 9, 10, 11, 9, 8, 6, 7, 9, 10, 6, 8]  # Demanda por dia
custo_permanente = 100  # Custo por dia de um trabalhador permanente
custo_temporario = 150  # Custo por dia de um trabalhador temporário

# Modelo
modelo = ConcreteModel()

# Variáveis
modelo.x = Var(dias, trabalhadores_permanentes, domain=Binary)  # Permanentes
modelo.y = Var(dias, domain=NonNegativeIntegers)  # Temporários

# Função objetivo: Minimizar custos
modelo.objetivo = Objective(
    expr=sum(custo_permanente * modelo.x[d, s] for d in dias for s in trabalhadores_permanentes) +
         sum(custo_temporario * modelo.y[d] for d in dias),
    sense=minimize
)

# Restrições de demanda
modelo.restricao_demanda = ConstraintList()
for d in dias:
    modelo.restricao_demanda.add(
        sum(modelo.x[d, s] for s in trabalhadores_permanentes) + 
      modelo.y[d] >= demanda[d]
    )

# Restrição de no máximo 7 dias consecutivos para permanentes
modelo.restricao_consecutivos = ConstraintList()
for s in trabalhadores_permanentes:
    for d in range(len(dias) - 7):
        modelo.restricao_consecutivos.add(
            sum(modelo.x[d + k, s] for k in range(8)) <= 7
        )

# Restrições para forçar folgas escalonadas
# Dia 4 (índice 3) trabalhador 1 não trabalha
modelo.fix_folga_1 = Constraint(expr=modelo.x[3, 0] == 0)
# Dia 5 (índice 4) trabalhador 2 não trabalha
modelo.fix_folga_2 = Constraint(expr=modelo.x[4, 1] == 0)
# Dia 6 (índice 5) trabalhador 3 não trabalha
modelo.fix_folga_3 = Constraint(expr=modelo.x[5, 2] == 0)
# Dia 7 (índice 6) trabalhador 4 não trabalha
modelo.fix_folga_4 = Constraint(expr=modelo.x[6, 3] == 0)
# Dia 8 (índice 7) trabalhador 5 não trabalha
modelo.fix_folga_5 = Constraint(expr=modelo.x[7, 4] == 0)

# Resolução
solver = SolverFactory('glpk')
resultado = solver.solve(modelo)

# Processamento dos resultados
custo_total = modelo.objetivo()

# Escalonamento de permanentes
escalonamento_permanentes = {
    f"Trabalhador {s + 1}": [int(modelo.x[d, s].value) for d in dias]
    for s in trabalhadores_permanentes
}

# Número de temporários por dia
temporarios = [int(modelo.y[d].value) for d in dias]

# Exibição dos resultados
print("Resultado da otimização:")
print(f"Custo total mínimo: R$ {custo_total:.2f}\n")

print("Escalonamento dos trabalhadores permanentes:")
for s in trabalhadores_permanentes:
    print(f"Trabalhador {s+1}: {escalonamento_permanentes[f'Trabalhador {s+1}']}")

print("\nNúmero de trabalhadores temporários por dia:")
for d in dias:
    print(f"Dia {d+1}: {temporarios[d]} temporários")

# DataFrame com o resultado final
resultado_df = pd.DataFrame(escalonamento_permanentes)
resultado_df["Temporários"] = temporarios
resultado_df["Demanda"] = demanda

print("\nTabela final:")
print(resultado_df)

Sortie :

Références :

XU, Karl; DU PREEZ, Johan; DAVARI, Hossein. Vers le jumeau numérique : une approche semi-automatique pour la modélisation d'usine basée sur des nuages de points. International Journal on Interactive Design and Manufacturing (IJIDeM), [S.l.], 2024.
Disponible en : https://doi.org/10.1007/s12008-024-02010-x.

WU, Haixin; CHENG, Yu; YANG, Xin; SU, Yuelong; XU, Jinxin; WANG, Liyang; FU, Xintong. Optimisation de la Planification des Travailleurs dans les Dépôts Logistiques en Utilisant des Algorithmes Génétiques et le Recuit Simulé. 2024. Disponible en : https://arxiv.org/pdf/2405.11729.