Soluciones

Blog

Nosotros

FAQ

Contacto

Select Language

Iniciar sesión

Solicitar demo

8 dic 2024

Optimización de Turnos Laborales

Imagina un almacén logístico que opera 24 horas al día. Cada hora, el número de paquetes a procesar varía, lo que hace crucial tener la cantidad adecuada de trabajadores para garantizar que todo se complete a tiempo. Contratar más personal del necesario aumenta los costos. Por otro lado, tener muy pocos trabajadores puede llevar a retrasos y a la insatisfacción del cliente.

Trabajadores Permanentes vs. Temporales

Las empresas dependen de dos tipos de trabajadores:

Trabajadores Permanentes: Personal a tiempo completo con más experiencia y eficiencia.
Trabajadores Temporales: Contratados según se necesite, son más costosos y menos eficientes, pero ofrecen flexibilidad.

El gran desafío es encontrar el equilibrio ideal entre estos dos grupos para satisfacer la demanda sin desperdiciar recursos.

Resolviendo el Rompecabezas con Modelos Matemáticos

Los investigadores han desarrollado modelos matemáticos para determinar la mejor manera de escalar la fuerza laboral. Utilizan una técnica llamada programación lineal entera 0-1, que, en pocas palabras, es una manera de representar decisiones (como "asignar un trabajador o no") utilizando ecuaciones matemáticas.

Objetivos del Modelo

Minimizar el total de días-trabajador para reducir los costos laborales.
Cumplir con la demanda horaria, asegurando suficientes trabajadores para cada turno.
Ajustarse a las restricciones, como no exceder el máximo de días de trabajo consecutivos para empleados permanentes y evitar programar a un trabajador para más de un turno por día.

Algoritmos Inteligentes para la Optimización

Resolver estos modelos matemáticos en la práctica puede ser muy complejo, especialmente cuando se trata de cientos o miles de trabajadores y turnos. Aquí es donde entran los algoritmos inteligentes:

Algoritmo Genético: Inspirado en la evolución natural, crea múltiples "soluciones candidatas" y combina las mejores partes de cada una para encontrar la solución óptima a lo largo del tiempo.
Recocido Simulado: Basado en el proceso de calentamiento y enfriamiento de metales, explora diferentes soluciones, aceptando ocasionalmente las menos óptimas para evitar quedar atrapado y, en última instancia, encontrar la mejor solución global.

Sistemas de Fabricación Reconfigurables

La optimización de la programación es crucial en las fábricas modernas, especialmente aquellas que utilizan Sistemas de Fabricación Reconfigurables (RMS). Estos sistemas pueden ajustarse rápidamente para producir diferentes productos o manejar variaciones en la demanda.

Desafíos Adicionales

Riesgos en el Lugar de Trabajo: Garantizar la seguridad de los trabajadores considerando los riesgos relacionados con las máquinas, así como la experiencia y capacitación de los empleados.
Preferencias de los Trabajadores: Ofrecer horarios flexibles puede aumentar la satisfacción y productividad de los empleados.

Modelo Multi-Objetivo

Para abordar estos desafíos, los investigadores han desarrollado un modelo dirigido a:

Minimizar el Tiempo Total de Producción (Makespan): Asegurando que los productos se fabriquen en el menor tiempo posible.
Minimizar el Costo Total de Producción: Incluyendo costos operativos y laborales.
Maximizar la Sostenibilidad Social: Mejorando la seguridad y satisfacción de los trabajadores.

Soluciones Avanzadas con Algoritmos Evolutivos

Para resolver este modelo complejo, se emplean algoritmos evolutivos avanzados:

NSGA-II: Un algoritmo multi-objetivo que encuentra soluciones óptimas de manera eficiente considerando múltiples objetivos simultáneamente.
AMOSA: Otro algoritmo multi-objetivo diseñado para una optimización efectiva bajo condiciones complejas.

Descripción General de NSGA-II

Los algoritmos genéticos (GAs) se encuentran entre los métodos de optimización metaheurística más utilizados y se han aplicado a una variedad de dominios. Pertenecen a un grupo de técnicas de inteligencia computacional inspiradas en principios evolutivos, codificando soluciones potenciales en estructuras similares a cromosomas. Al emplear varios operadores reproductivos, como el cruce y la mutación, los GAs preservan información clave dentro de cada cromosoma mientras generan nuevas soluciones candidatas.

Para abordar los desafíos de optimización multi-objetivo, los GAs requieren un sistema de clasificación basado en vectores para identificar soluciones efectivas. Uno de los métodos de clasificación de vectores más destacados combinado con GAs es la clasificación no dominada. Introducida por Srinivas y Deb, este enfoque —denominado NSGA— aplica la clasificación no dominada para abordar problemas multi-objetivo.

No obstante, NSGA enfrenta tres desventajas principales:

El procedimiento de clasificación no dominada consume mucho tiempo y es costoso computacionalmente.
Determinar parámetros de compartir apropiados es un desafío.
La falta de elitismo puede resultar en la pérdida de soluciones de alta calidad una vez que han sido encontradas.

Para superar estas limitaciones, Deb desarrolló NSGA-II. Los pasos principales de NSGA-II se describen en el siguiente algoritmo.

Durante la etapa de cruce, los genes de los cromosomas progenitores se seleccionan para crear nuevas crías. El enfoque más simple implica elegir un punto de cruce al azar. Sin modificaciones, los valores del cromosoma antes y después de este punto se transmiten directamente a la descendencia, mientras que los valores entre los puntos elegidos se intercambian entre los padres correspondientes para producir las nuevas soluciones.

# Pseudocódigo para um algoritmo genético baseado em NSGA-II

# Parâmetros necessários:
# population_size, total_iterations, crossover_probability, 
# mutation_probability

# 1: Geração da solução inicial aleatória
population = generate_initial_population(population_size)

# 2: Avaliar valores objetivos
evaluate_population(population)

# 3: Atribuir rank baseado em Pareto
pareto_sort(population)

# 4: Gerar população de descendentes
offspring = generate_offspring(population, crossover_probability, 
                               mutation_probability)

# 5: Seleção por torneio binário
selected_parents = binary_tournament_selection(population)

# 6: Crossover e mutação
offspring = apply_crossover_and_mutation(selected_parents, 
                                         crossover_probability, 
                                         mutation_probability)

# 7: Início das iterações
for iteration in range(total_iterations):
    # 8: Para pais e filhos na população
    combined_population = population + offspring

    # 9: Regenerar nova população utilizando crossover e mutação
    offspring = apply_crossover_and_mutation(combined_population, 
                                             crossover_probability, 
                                             mutation_probability)

    # 10: Cálculo do valor de aptidão (fitness) de toda a população
    evaluate_population(combined_population)

    # 11: Ordenar soluções usando mecanismo de ordenação não-dominado
    pareto_fronts = non_dominated_sorting(combined_population)

    # 12: Adicionar soluções à próxima geração, partindo da primeira fronteira
    next_population = []
    for front in pareto_fronts:
        if len(next_population) + len(front) <= population_size:
            next_population.extend(front)
        else:
            next_population.extend(select_by_crowding_distance(front, 
                                                               population_size - 
                                                               len(next_population)))
            break

    # 14: Selecionar pontos da fronteira inferior com alta distância de aglomeração (já realizado acima)
    # 15: Criar próxima geração
    population = next_population

    # 16: Seleção por torneio binário
    selected_parents = binary_tournament_selection(population)

    # 17: Crossover e mutação
    offspring = apply_crossover_and_mutation(selected_parents, 
                                             crossover_probability, 
                                             mutation_probability)

# 18: Fim das iterações

Descripción General de AMOSA

Bandyopadhyay introdujo una técnica de optimización multi-objetivo basada en el recocido simulado, conocida como AMOSA. Este método emplea una estructura de archivo para producir un conjunto de soluciones de compromiso. Los autores idearon un procedimiento innovador que toma en cuenta el estado de dominio para determinar la probabilidad de retener una nueva solución candidata generada. El pseudocódigo para la AMOSA adaptada se presenta en el Algoritmo 2

# Pseudocódigo para um Algoritmo de Otimização Multiobjetivo Baseado em Arquivo

# Parâmetros necessários:
# Tmax, Tmin, iter, α (alpha), temp = Tmax
# É necessário também uma razão de perturbação (perturbation ratio)
# Archive: coleção de pontos (soluções) já conhecidos

Current_points = random_selection_from(Archive)
temp = Tmax

while temp > Tmin:
    for i in range(iter):
        New_points = perturb(Current_points)

        # Se Current_points domina New_points
        if dominates(Current_points, New_points):
            # New_points = Current_points com alguma probabilidade
            if should_replace():
                New_points = Current_points

        # Se Current_points e New_points não dominam um ao outro
        if non_dominating(Current_points, New_points):

            # Se New_points é dominado por k pontos no Archive
            if dominated_by_k_points_in_archive(New_points, Archive):
                # New_points = Current_points com alguma probabilidade
                if should_replace():
                    New_points = Current_points

            # Se nenhum ponto no Archive domina New_points
            if no_point_in_archive_dominates(New_points, Archive):
                New_points = Current_points
                add_to_archive(New_points, Archive)
                remove_dominated_by(New_points, Archive)

        # Se New_points domina Current_points
        if dominates(New_points, Current_points):
            New_points = Current_points
            add_to_archive(New_points, Archive)
            remove_dominated_by(New_points, Archive)

    temp = temp * α

return Archive

AUGMECON-R: Un método exacto diseñado para ayudar a identificar el conjunto de soluciones eficientes (frontera de Pareto) para problemas multi-objetivo.

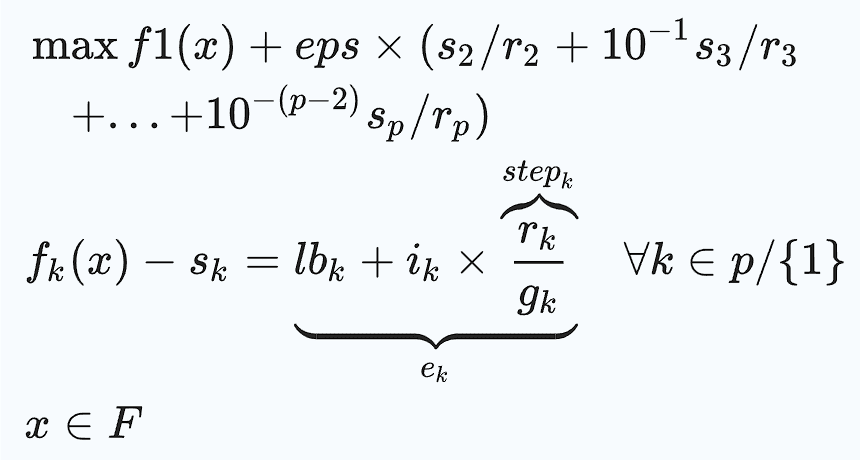
lbk denota el límite inferior del k-ésimo objetivo, rk representa el rango del k-ésimo objetivo, gk indica el número de intervalos para el k-ésimo objetivo, y sk es la variable de holgura asociada con el k-ésimo objetivo. El parámetro EPS es un número muy pequeño, generalmente elegido dentro del intervalo (10⁻⁶, 10⁻³), y F representa la región factible. En cada iteración del algoritmo, se calculan los coeficientes de bypass bi = int(si / stepi).

Si si ≥ stepi, entonces la iteración subsiguiente para bi', donde ei' = si - stepi, daría como resultado la misma solución. Dado que si' = si - stepi, esa iteración puede considerarse redundante. En otras palabras, el coeficiente de bypass bi dicta cuántas iteraciones deben omitirse.

Durante cada iteración del bucle principal, el algoritmo mantiene una matriz de banderas, flag[(g2 + 1) × (g3 + 1) × ... × (gp + 1)]. Inicialmente, esta matriz se establece en cero. El algoritmo verifica la entrada de la matriz antes de realizar cualquier optimización: si la entrada actual es cero, procede con la optimización; si no, omite el número de iteraciones especificado por el valor no cero en la matriz para el bucle más interno.

Ejemplo Simple Usando un Solver de Código Abierto

Descripción del Problema

Objetivo: Minimizar el total de días-trabajador utilizados.

Trabajadores:

Trabajadores Permanentes: Empleados a tiempo completo con restricciones en los días de trabajo consecutivos.
Trabajadores Temporales: Contratados según se necesite, sin restricciones en los días de trabajo consecutivos.

Demandas:

Variación diaria en la demanda de trabajadores.
Necesidad de satisfacer la demanda para cada día operativo.

Restricciones:

Cada trabajador puede trabajar un máximo de un turno por día.
Los trabajadores permanentes no pueden trabajar más de 7 días consecutivos.
Límites en las horas trabajadas por día y por semana.

Modelado en Python

Aquí, utilizamos el modelo directamente para resolver el problema, ya que estamos tratando con un número reducido de trabajadores.

from pyomo.environ import *
from pyomo.opt import SolverFactory
import pandas as pd

# Dados do problema
dias = list(range(14))  # 14 dias
trabalhadores_permanentes = list(range(5))  # 5 trabalhadores permanentes
demanda = [8, 6, 7, 9, 10, 11, 9, 8, 6, 7, 9, 10, 6, 8]  # Demanda por dia
custo_permanente = 100  # Custo por dia de um trabalhador permanente
custo_temporario = 150  # Custo por dia de um trabalhador temporário

# Modelo
modelo = ConcreteModel()

# Variáveis
modelo.x = Var(dias, trabalhadores_permanentes, domain=Binary)  # Permanentes
modelo.y = Var(dias, domain=NonNegativeIntegers)  # Temporários

# Função objetivo: Minimizar custos
modelo.objetivo = Objective(
    expr=sum(custo_permanente * modelo.x[d, s] for d in dias 
             for s in trabalhadores_permanentes) +
         sum(custo_temporario * modelo.y[d] for d in dias),
    sense=minimize
)

# Restrições de demanda
modelo.restricao_demanda = ConstraintList()
for d in dias:
    modelo.restricao_demanda.add(
        sum(modelo.x[d, s] for s in trabalhadores_permanentes) + 
      modelo.y[d] >= demanda[d]
    )

# Restrição de no máximo 7 dias consecutivos para permanentes.
modelo.restricao_consecutivos = ConstraintList()
for s in trabalhadores_permanentes:
    for d in range(len(dias) - 7):
        modelo.restricao_consecutivos.add(
            sum(modelo.x[d + k, s] for k in range(8)) <= 7
        )

# Resolução
solver = SolverFactory('glpk')
resultado = solver.solve(modelo)

# Processamento dos resultados
custo_total = modelo.objetivo()

# Escalonamento de permanentes
escalonamento_permanentes = {
    f"Trabalhador {s + 1}": [int(modelo.x[d, s].value) for d in dias]
    for s in trabalhadores_permanentes
}

# Número de temporários por dia
temporarios = [int(modelo.y[d].value) for d in dias]

# Apresentar os resultados
print("Resultado da otimização:")
print(f"Custo total mínimo: R$ {custo_total:.2f}\n")

print("Escalonamento dos trabalhadores permanentes:")
for s in trabalhadores_permanentes:
    print(f"Trabalhador {s+1}: {escalonamento_permanentes[f'Trabalhador {s+1}']}")

print("\nNúmero de trabalhadores temporários por dia:")
for d in dias:
    print(f"Dia {d+1}: {temporarios[d]} temporários")

# DataFrame com o resultado final
resultado_df = pd.DataFrame(escalonamento_permanentes)
resultado_df["Temporários"] = temporarios
resultado_df["Demanda"] = demanda

print("\nTabela final:")
print(resultado_df)

Salida:

Estos resultados muestran que el modelo utilizó siempre a los 5 trabajadores permanentes durante el máximo de días consecutivos permitidos. Cuando fue necesario darles un descanso colectivo (para evitar exceder el límite de trabajo consecutivo de 7 días), dependió en gran medida de los trabajadores temporales durante ese día de descanso. Esto resultó en un patrón donde se requerían muchos trabajadores temporales en ciertos días (por ejemplo, el Día 7) y pocos o ninguno en otros, satisfaciendo la demanda pero de manera concentrada y menos realista desde una perspectiva operacional.

A continuación se presenta un ejemplo de código de Python + Pyomo similar al anterior, pero forzando un enfoque de programación más realista. Para lograr esto, agregamos restricciones que asignan días de descanso específicos para cada trabajador permanente (en lugar de permitir que el solver decidiera libremente, lo que previamente llevó a que todos los trabajadores tuvieran el mismo día libre). Con estas restricciones, cada trabajador tiene un día de descanso escalonado, evitando que todos los trabajadores permanentes necesiten descansar simultáneamente.

El Trabajador 1 descansa el Día 4
El Trabajador 2 descansa el Día 5
El Trabajador 3 descansa el Día 6
El Trabajador 4 descansa el Día 7
El Trabajador 5 descansa el Día 8

from pyomo.environ import *
from pyomo.opt import SolverFactory
import pandas as pd

# Dados do problema
dias = list(range(14))  # 14 dias
trabalhadores_permanentes = list(range(5))  # 5 trabalhadores permanentes
demanda = [8, 6, 7, 9, 10, 11, 9, 8, 6, 7, 9, 10, 6, 8]  # Demanda por dia
custo_permanente = 100  # Custo por dia de um trabalhador permanente
custo_temporario = 150  # Custo por dia de um trabalhador temporário

# Modelo
modelo = ConcreteModel()

# Variáveis
modelo.x = Var(dias, trabalhadores_permanentes, domain=Binary)  # Permanentes
modelo.y = Var(dias, domain=NonNegativeIntegers)  # Temporários

# Função objetivo: Minimizar custos
modelo.objetivo = Objective(
    expr=sum(custo_permanente * modelo.x[d, s] for d in dias for s in trabalhadores_permanentes) +
         sum(custo_temporario * modelo.y[d] for d in dias),
    sense=minimize
)

# Restrições de demanda
modelo.restricao_demanda = ConstraintList()
for d in dias:
    modelo.restricao_demanda.add(
        sum(modelo.x[d, s] for s in trabalhadores_permanentes) + 
      modelo.y[d] >= demanda[d]
    )

# Restrição de no máximo 7 dias consecutivos para permanentes
modelo.restricao_consecutivos = ConstraintList()
for s in trabalhadores_permanentes:
    for d in range(len(dias) - 7):
        modelo.restricao_consecutivos.add(
            sum(modelo.x[d + k, s] for k in range(8)) <= 7
        )

# Restrições para forçar folgas escalonadas
# Dia 4 (índice 3) trabalhador 1 não trabalha
modelo.fix_folga_1 = Constraint(expr=modelo.x[3, 0] == 0)
# Dia 5 (índice 4) trabalhador 2 não trabalha
modelo.fix_folga_2 = Constraint(expr=modelo.x[4, 1] == 0)
# Dia 6 (índice 5) trabalhador 3 não trabalha
modelo.fix_folga_3 = Constraint(expr=modelo.x[5, 2] == 0)
# Dia 7 (índice 6) trabalhador 4 não trabalha
modelo.fix_folga_4 = Constraint(expr=modelo.x[6, 3] == 0)
# Dia 8 (índice 7) trabalhador 5 não trabalha
modelo.fix_folga_5 = Constraint(expr=modelo.x[7, 4] == 0)

# Resolução
solver = SolverFactory('glpk')
resultado = solver.solve(modelo)

# Processamento dos resultados
custo_total = modelo.objetivo()

# Escalonamento de permanentes
escalonamento_permanentes = {
    f"Trabalhador {s + 1}": [int(modelo.x[d, s].value) for d in dias]
    for s in trabalhadores_permanentes
}

# Número de temporários por dia
temporarios = [int(modelo.y[d].value) for d in dias]

# Exibição dos resultados
print("Resultado da otimização:")
print(f"Custo total mínimo: R$ {custo_total:.2f}\n")

print("Escalonamento dos trabalhadores permanentes:")
for s in trabalhadores_permanentes:
    print(f"Trabalhador {s+1}: {escalonamento_permanentes[f'Trabalhador {s+1}']}")

print("\nNúmero de trabalhadores temporários por dia:")
for d in dias:
    print(f"Dia {d+1}: {temporarios[d]} temporários")

# DataFrame com o resultado final
resultado_df = pd.DataFrame(escalonamento_permanentes)
resultado_df["Temporários"] = temporarios
resultado_df["Demanda"] = demanda

print("\nTabela final:")
print(resultado_df)

Salida:

Referencias:

XU, Karl; DU PREEZ, Johan; DAVARI, Hossein. Hacia el gemelo digital: un enfoque semiautomático para la modelización de fábricas basadas en nubes de puntos. International Journal on Interactive Design and Manufacturing (IJIDeM), [S.l.], 2024.
Disponible en: https://doi.org/10.1007/s12008-024-02010-x.

WU, Haixin; CHENG, Yu; YANG, Xin; SU, Yuelong; XU, Jinxin; WANG, Liyang; FU, Xintong. Optimización de la programación de trabajadores en depósitos logísticos utilizando algoritmos genéticos y recocido simulado. 2024. Disponible en: https://arxiv.org/pdf/2405.11729.